Understanding Confidence Intervals Easy Examples And Formulas by Rebecca Bevans

What is there always when you make an estimate in statistics and why?
When you make an estimate in statistics, there is always uncertainty around that estimate because the number is based on a sample of the population you're studying.

What is the confidence interval?
The confidence interval is a range of values you expect your estimate to fall between a certain percentage of the time if you run your experiment again or re-sample the population in the same way.

What is the confidence level?
The confidence level is the percentage of times you expect to reproduce an estimate between the upper and lower bounds of the confidence interval.

What is the confidence level set by?
The confidence level is set by the alpha value.

What exactly is a confidence level?

What makes up the confidence level?
The confidence level is made up of the mean of your estimate plus and minus the variation in that estimate.

What is confidence in statistics?
Confidence in statistics is another way to describe probability.

If you construct a confidence interval with a 95% confidence level, you are confident that ... out of ... times the estimate will fall between the ... and ... values specified by the confidence interval.
If you construct a confidence interval with a 95% confidence level, you are confident that 95 out of 100 times the estimate will fall between the upper and lower values specified by the confidence interval.

How is the desired confidence level typically calculated?
The desired confidence level is typically calculated by subtracting the alpha value you used in your statistical test from 1.

Example of calculating the desired confidence level

If you used an alpha value of for statistical significance, then your confidence level would be or 95%.

When do you use confidence intervals?

What are some statistical estimates you can calculate confidence intervals for?
Some statistical estimates you can calculate confidence intervals for include:

  • Proportions.
  • Population means.
  • Differences between population means and proportions.
  • Estimates of variation among groups.
Note

What Is A Point Estimate by Zach Bobbitt

Why are confidence intervals useful for point estimates?
Confidence intervals are useful for point estimates because point estimates don't give any information about the variation around the number.

Example of variation around a point estimate with a TV-watching survey

100 Brits and 100 Americans are surveyed about their TV watching habits. The average of both samples is 35 hours per week. However, there was wider variation in the number of hours watched with the British. The Americans in the other sample watched TV in similar amounts of time. Despite the point estimate being the same, the British sample will have a higher confidence interval than the American estimate because there's more variation in the data.

Calculating a confidence interval: what you need to know

Most ... ... will include the confidence interval of the estimate when you run a statistical test.
Most statistical programs will include the confidence interval of the estimate when you run a statistical test.

What four things do you need to know to calculate the confidence interval?
To calculate the confidence interval, the four things you need to know are:

  1. The point estimate you are constructing the confidence interval for.
  2. The critical values for the test statistic.
  3. The standard deviation of the sample.
  4. The sample size.

What do you do with the four components to calculate the confidence interval?
To calculate the confidence interval with the four components, you plug them into the confidence interval formula which corresponds to your data.

Point estimate

What is the point estimate?
The point estimate is the statistical estimate you're making.

Example of the point estimate with the TV-watching survey

The point estimate from the TV-watching survey is the mean of the number of hours watched: 35.

Finding the critical value

What do critical values tell you?
Critical values tell you how many standard deviations away from the mean you need to go in order to reach the desired confidence level for your confidence interval.

How do you find the critical values?
To find the critical values:

  1. Choose your alpha () value.
  2. Decide if you need a one-tailed or two-tailed interval.
  3. Look up the critical value that corresponds with the alpha value.

What is the alpha () value?
The value is the probability threshold for statistical significance.

What is the most common alpha () value?
The most common alpha () value is .

What are three other values which aren't as common but are still used as alpha () values?
Three other values which aren't as common but are still used as values include:

  1. 0.1
  2. 0.01.
  3. 0.001.

What's the best way to pick the alpha () value?
The best way to pick the value is to look at research papers in your field.

Will you most likely use a one-tailed or two-tailed interval?
You will most likely use a one-tailed interval.

When would you use a one-tailed interval?
You would use a one-tailed interval if you're doing a one-tailed test.

What do you do with the alpha () value if you're using a two-tailed interval?
If you're using a two-tailed interval, you divide the value by two.

When do you use the z distribution to find the critical values?
You use the z distribution to find the critical values if you have a large sample size () that is approximately normally distributed.

What are the most common values for a z statistic?
The most common values for a z statistic are:

For One-Tailed CI For Two-Tailed CI Z Statistic
0.1 0.05 1.64
0.05 0.025 1.96
0.01 0.005 2.57

When do you use the t distribution to find the critical values?
You use the t distribution to find the critical values if you have a small sample size () that is approximately normally distributed.

How is the t distribution similar to the z distribution?
The t distribution is similar to the z distribution in that both follow the same shape.

How is the t distribution different from the z distribution?
The t distribution is different from the z distribution in that it accounts for small sample sizes.

What do you need to know to use the t distribution?
To use the t distribution, you need to know your degrees of freedom (sample size minus one).

Todo (1)

This section includes a link to a set of t tables which can be used to find the t statistic.

For normal distributions, like the t distribution and z distribution, the critical value is ... ... on either side of the mean.
For normal distributions, like the t distribution and z distribution, the critical value is the same on either side of the mean.

Example of finding the critical value with the TV-watching survey

There are more than 30 observations and the data follows an approximately normal distribution (bell curve), so you can use the z distribution for the test statistics.

For a two-tailed 95% confidence interval, the alpha value is 0.025 and the corresponding critical value is 1.96.

The upper and lower bounds of the confidence interval are standard deviations from the mean.

Finding the standard deviation

How do you find the standard deviation?
To find the standard deviation:

  1. Find the sample variance.
  2. Take the square root of the sample variance.

What is the sample variance?
The sample variance is the sum of squared differences from the mean, or the mean-squared-error (MSE).

What is the formula for the Mean-Squared-Error (MSE)?
The formula for the MSE is:

What are the variables in the formula for the Mean-Squared-Error (MSE)?
The variables in the formula for the MSE are:

  • - The sample variance, which is equivalent to the standard deviation squared.
  • - The sample size.
  • - Represents the position of a value in the dataset.
  • - A value in the dataset which is at position .
  • - The population mean.
Example of finding the standard deviation with the TV-watching survey

The variance in the British sample is 100. The variance in the American sample is 25. Taking the square root of the variance gives a standard deviation of 10 for the British sample and 5 for the American sample.

Sample size

What is the sample size?
The sample size is the number of observations in a data set.

Confidence interval for the mean of normally-distributed data

What shape does normally-distributed data form when plotted on a graph?
When plotted on a graph, normally-distributed data forms a bell shape.

What is the formula for the confidence interval around the mean of normally-distributed data?
The formula for the confidence interval around the mean of normally-distributed data is:

What are the variables in the formula for the confidence interval for the mean of normally-distributed data?
The variables in the formula for the confidence interval for the mean of normally-distributed data are:

  • - The confidence interval.
  • - The population mean.
  • - The critical value of the z distribution.
  • - The population standard deviation.
  • - The square root of the population size.

What is the formula for the confidence interval around the mean of a sample of normally-distributed data?
The formula for the confidence interval around the mean of a sample of normally-distributed data is:

What are the variables in the formula for the confidence interval around the mean of a sample of normally-distributed data?
The variables in the formula for the confidence interval around the mean of a sample of normally-distributed data are:

  • - The confidence interval.
  • - The sample mean.
  • - The critical value of the z distribution.
  • - The sample standard deviation.
  • - The square root of the population size.
Example of calculating the confidence interval with the TV-watching survey

For the British sample:
For the American sample:

Confidence interval for proportions

What is the formula for the confidence interval around a proportion?
The formula for the confidence interval around a proportion is:

What are the variables in the formula for the confidence interval around a proportion?
The variables in the formula for the confidence interval around a proportion are:

  • - The confidence interval.
  • - The proportion in the sample.
  • - The critical value of the z distribution.
  • - The square root of the population size.

Confidence interval for non-normally distributed data

What are the two options for calculating the confidence interval around the mean of non-normally distributed data?
The two options for calculating the confidence interval around the mean of non-normally distributed data are:

  1. Finding the distribution which matches the shape of your data and using it to calculate the confidence interval.
  2. Transforming the data to make it fit a normal distribution and then finding the confidence interval.

Is performing data transformations common in statistics?
Yes, performing data transformation is very common in statistics.

What do you have to do with the transformed data when calculating the upper and lower bounds of the confidence interval?
When calculating the upper and lower bounds of the confidence interval, you have to perform the reverse transformation on the data.

Reporting confidence intervals

Do researchers report on the confidence interval or standard deviation of their estimate more often?
More often, researchers report the standard deviation of their estimate.

What should you include if you're asked to report the confidence interval?
If you're asked to report the confidence interval, you should include the upper and lower bounds.

Example of reporting the confidence level with the TV-watching survey

“We found that both the US and Great Britain averaged 35 hours of television watched per week, although there was more variation in the estimate for Great Britain (95% CI  = 33.04, 36.96) than for the US (95% CI = 34.02, 35.98).”

What is one place where confidence intervals are frequently used?
One place where confidence intervals are frequently used is in graphs.

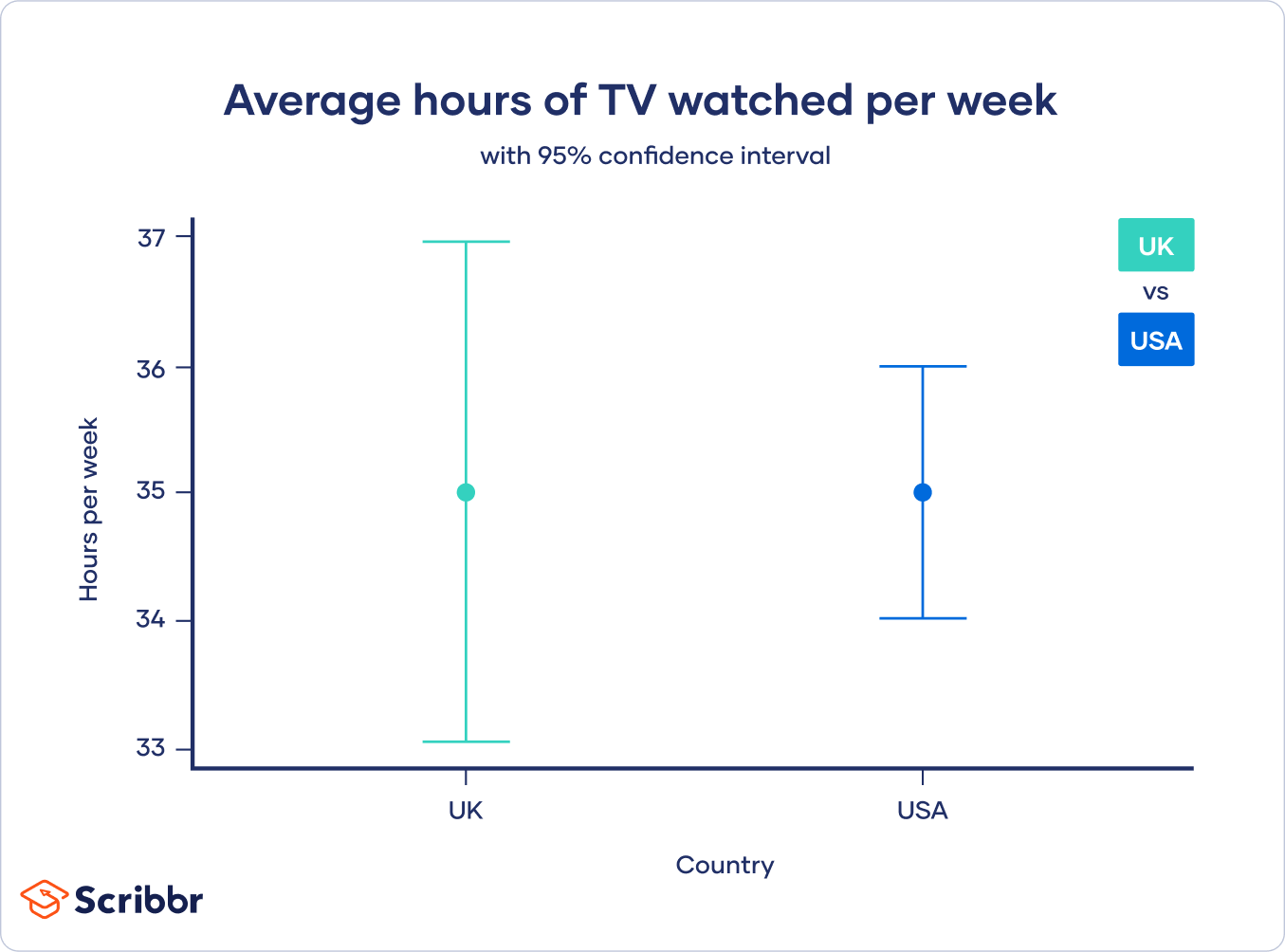
Example of including the confidence interval in a graph with the TV-watching survey

Caution when using confidence intervals

What is a common misinterpretation of confidence intervals?
A common misinterpretation of confidence intervals is that the true value of the estimate lies within the bounds of the confidence interval.

What is the only thing the confidence interval can tell you?
The only thing the confidence interval can tell you is what range of values you can expect to find if you re-do your sampling and run your experiment again in the exact same way.

What two factors would determine the likelihood of your confidence interval including the true value of your estimate?
Two factors that would determine the likelihood of your confidence interval including the true value of your estimate are:

  1. How accurate your sampling plan is.
  2. How realistic your experiment is.

What determines the accuracy of your sampling plan or how realistic your experiment is?
The accuracy of your sampling plan or how realistic your experiment is are determined by your research methods.

...